Solving Bayesian Inverse Problems via Variational Autoencoders
Major Activities:
From divergence-based variational inference, we have constructed an effective solution for Bayesian inverse problems using the variational autoencoder(VAE) approach such that most of the information usually present in scientific inverse problems is fully utilized in the training procedure. Additionally, this framework includes an adjustable hyperparameter that allows selection of the notion of distance between the posterior model and the target distribution. This introduces more flexibility in controlling how optimization directs the learning of the posterior model. Further, this framework possesses an inherent adaptive optimization property that emerges through the learning of the posterior uncertainty.
Specific Objectives:
Develop a new variational autoencoder approach for fast solution to Bayesian inverse problems. In particular, we leverage and adapt the VAE for a different purpose: uncertainty quantification in scientific inverse problems. In doing so, we obtain what we call UQ-VAE: a flexible, adaptive, hybrid data/model-informed framework for training neural networks capable of rapid modelling of the posterior distribution representing the unknown parameter of interest. Due to its generative modelling nature, once our UQ-VAE network is trained, it can be used to generate as many samples of the posterior as we wish with negligible cost.
Significant Results:
For generative modelling, the focus of training VAEs is to learn the generating function. In contrast, for scientific inverse problems, the PtO map need not be learnt as it can often be modelled using physics-based numerical methods.
For generative modelling, the latent space of VAEs is an unspecified quantity with properties emerging almost entirely though the process of learning the generating function. In contrast, for scientific inverse problems, by considering the latent space to be the solution space, the latent space therefore possesses structure that represents the physical properties of the PoI.
Therefore, in the context of scientific inverse problems, we possess more information that can be utilized to improve the training procedure of a VAE. Indeed, in reference to the first point, one can surrogate the generating map with physics-based numerical modelling of the PtO map. In doing so, the focus of the training is shifted completely towards inference. In reference to the second point, knowledge of the physical properties of the PoI can be encoded in the prior model which, therefore, allows for a more informative latent distribution than the isotropic Gaussian.
To derive the UQ-VAE framework, instead of the Kullback-Liebler Divergence (KLD) we elect to use the following family of Jensen-Shannon divergences (JSD):

In doing so, we obtain the following loss functional:
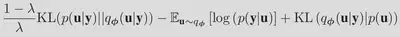
which, when employing Monte-Carlo approximations of the expectations, yields the following optimization problem:
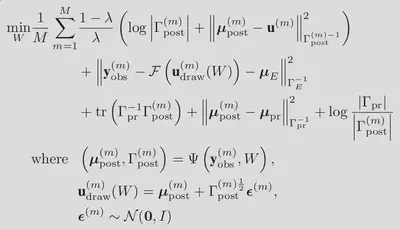
Thus, with only an adjustment of a single scalar value,
our framework allows the selection of the notion of distance used by the
optimization routine to direct the model posterior towards the target
posterior. Following the adoption of some statistical approximation for
the purposes of implementation, we expose that the adjustment of this
scalar value translates to control of the balance of data-fitting and
regularization used in the training procedure.
In order to produce results, we coded the UQ-VAE framework in
Tensorflow. To implement the PtO map, we extracted finite element
operators provided by the FEniCS finite element library
and cast it into a compatible object that can be
utilized by Tensorflow’s GPU accelerated neural network optimization
routines. For the case when a numerical model is used for the PtO map,
there are some issues with computational efficiency one must consider.
For comparison with traditional methods, we use the hIPPYlib library to
compute the Laplace approximation using gradients and Hessians derived
via the adjoint method, inexact Newton-CG, Armijo line search and
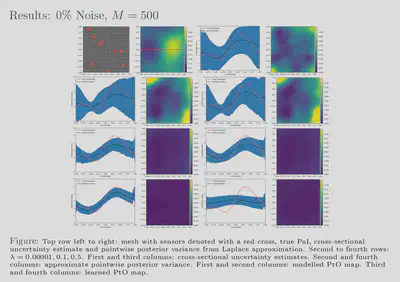
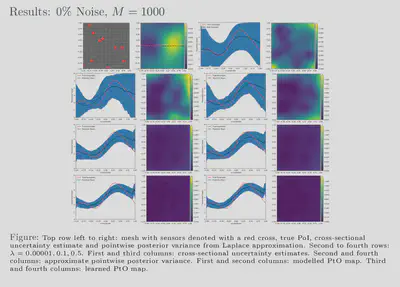
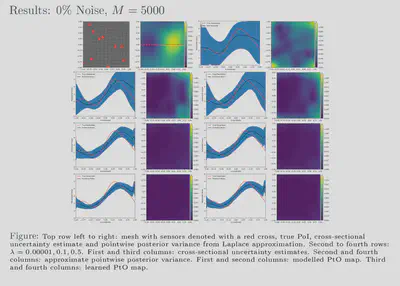
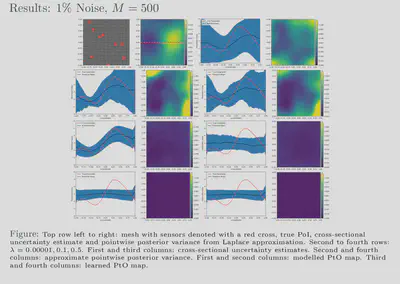
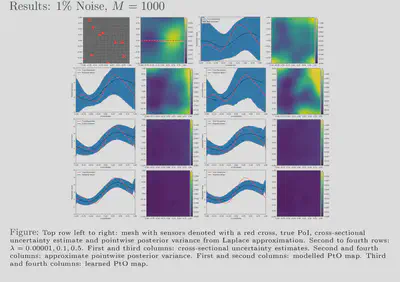
randomized eigensolvers. Our results also show that feasible estimates
are achievable with our framework for various noise levels and, further,
that these estimates exhibit behaviour similar to that of more
traditional methods. Additionally, our uncertainty estimates show a
favourable response to the size of our training dataset; the uncertainty
is inversely proportional to the amount of training data used which
reflects the availability or lack of information. We have showed that
our approach is 2750 times faster than the traditional approach while
giving comparable, in some cases better, results.