Are DNNs actually expressive?

Major Activities

Neural networks are function approximators whose parameters exist in a very high dimensional space. Because of the layered and strongly inter-connected nature of neural networks, analysis can be difficult. To this end, active subspaces are leveraged as a computational tool for analysis of characteristics of the parameter space for a given neural network. We introduce the concept of network condition number to measure the network expressiveness.

Significant Results

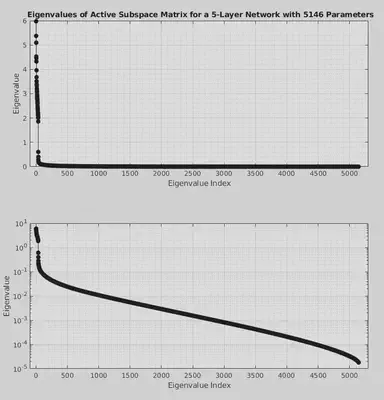
The first prominent finding is that all computation units are important.

The following figure illustrates the eigenvalues of the active subspace matrix for a network with 1 input neuron, 1 output neuron, and 5 hidden layers with 35 neurons per hidden layer, giving 5146 parameters total. The active subspace was estimated with ten thousand samples. The losses were calculated on a regression problem to regress a sin function.

The second prominent finding is that some network parameters are more important than others, in the sense that the loss is more sensitive to them than others.