Active subspaces data-informed approach for inverse problems

Major Activities

In the traditional inverse problem, the Tikhonov regularization method is often used, which penalizes equally all data modes. Recently, a few studies show that data-informed directions should be intact. Nevertheless, the important modes are determined using an eigendecomposition of the linear operator. There are two main drawbacks of such a method: (i) it only applies to a linear operator (limited to the linear problem), and (ii) it ignores observational data. In order to address these two issues we have developed an active subspace data-informed inversion approach. In particular, our method works for both linear and nonlinear operators.

Significant Results

Linear inverse problem (X-Ray imaging)

The orginal active subspace method is to detect the main data directions and then ignore the unimportant modes. Thus, we analyze both cases: (i)approximated misfit term (ii) full misfit term.

The former includes

ACT: the data misfit only considered acitve data modes.

ACT-M: the data misfit only considered acitve data modes and the active subspace matrix is substracted from the gradient mean.

The latter consists of

ACT-Full: the data misfit considered all data modes.

ACT-M-Full: the data misfit considered all data modes and the active subspace matrix is substracted from the gradient mean.

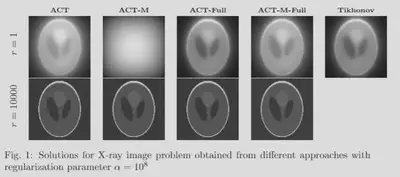
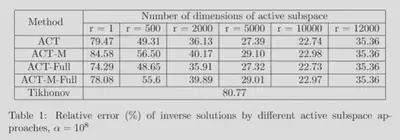
The figure 1 shows the obatained results by all four methods with very large regularization parameter, as opposed to the Tikhonov method (which is overregularized). Firstly, with one-dimensional active subspace, ACT, ACT-Full, and ACT-M-Full methods give better reconstructions than Tik. Secondly, in optimal rank, all methods are robust in terms of regulariation parameter. In other words, we can avoid overregularize the informed data modes. Table 1. presents the relative error of the inverse image.

Nonlinear PDE-constrained inverse problem

We now consider the poison 2D inverse problem in Hippylib package.

$$ \min_{m} \mathcal{J} := \frac{1}{2} \int_{\Omega} (u - u_d)^2 , dx + \frac{\gamma}{2} \int_{\Omega} | \nabla m|^2 , dx, $$

where $ u$ is the solution of the following PDE

$$ -\nabla \cdot (\exp(m) \nabla u) = f \quad \text{in} \quad \Omega$$

with boundary conditions

$$ u = 0 \quad \text{on} \quad \partial \Omega $$

Fig 2 shows that our active subspace data-informed approach outperforms the traditional Tikhonov inversion method.