Model constrained DNNs for inverse problems

Major Activities

In this project, we introduce several model-constrained approaches—including both feed-forward deep neural network (DNN) and autoencoders—that are capable of learning not only information hidden in the training data but also in the underlying mathematical models to solve inverse problems. We present and provide intuitions for our formulations for general nonlinear problems. For linear inverse problems and linear networks, the first-order optimality conditions show that our model-constrained deep learning (mcDL) approaches can learn information encoded in the underlying mathematical models and thus can produce consistent or equivalent inverse solutions.

Specific Objectives

The main idea is that we take advantage of the forward map G for regularizing the network. Moreover, we also expect that it is consistent with the form of the inverse solution; and thus, improving the accuracy of the training test. To have some intitutions of the method, let us look at the case of linear network and linear inverse problem with linear operator. The formulation of mcDNN approach is

$$ \min_{b,W} \frac{1}{2} | U - (WY + B) |_{\Gamma^{-1}}^2 +\frac{\alpha}{2} | Y -G (WY + B)|_{\Lambda^{-1}}^2.$$

The optimal solution of the DNN training problem can be shown to be exactly the solution of the following regularized linear inverse problem

$$ \min_{u} \frac{1}{2} \left|y_{\text{obs}} - G u\right|_{\Gamma^{-1}}^2 + \frac{1}{2\alpha} \left|u - u_0 \right|_{\Lambda^{-1}}^2, $$

where

$$ \textbf{u}_0 = \bar{\textbf{u}} +\bar{U} , \bar{Y}^{\dagger} (\textbf{y}_{\text{obs}} - \bar{\textbf{y}}) - \alpha \Gamma G^T \Lambda (I - \bar{Y} , \bar{Y}^{\dagger}) (\textbf{y}_{\text{obs}} - \bar{\textbf{y}}). $$

Significant Results

Linear problem for testing the derivation

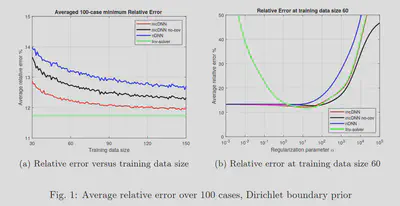
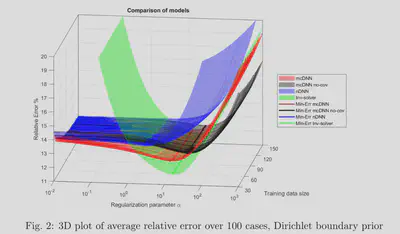
The results for the linear inverse problem with a linear neural network show that the model-constrained term added to the cost function gives better results than the naive DNN. In particular, the accuracy of naive DNN solely depends on how much training data we have. Meanwhile, as shown in the figure 1., with the same training data set, the mcDNN approach gives a lower error in the test data set.

Nonlinear PDE problems

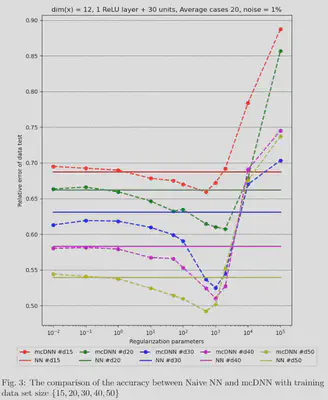
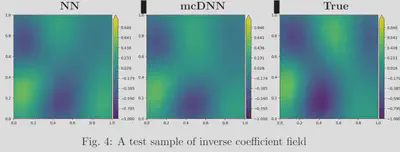
The results for training the conductivity coefficients for heat equation as shown in the firgure 3. It can be seen that with smaller training data set mcDNN approach is able to achive the same accuracy level compared to the naive DNN. An test sample of the inverse field obtained by Naive DNN and mcDNN is presented in the figure 4.

More detail about this work can be found at https://arxiv.org/abs/2105.12033.